树结构的概念
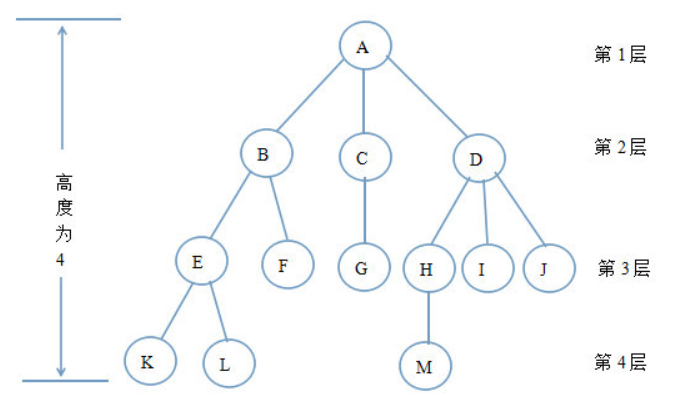
考虑结点 K 。 根 A 到结点 K 的唯一路径上的任意结点,称为结点 K 的祖先结点。
如结点 B 是结点 K 的祖先结点,而结点 K 是结点 B 的子孙结点。
路径上最接近结点 K 的结点 E 称为结点 K 的双亲结点,而结点 K 为结点 E 的孩子结点。
根 A 是树中唯一没有双亲的结点。
有相同双亲的结点称为兄弟结点,如结点 K 和结点 L 有相同的双亲结点,即 K 和 L 为兄弟结点。
树中一个结点的子结点个数称为该结点的度。
树中结点的最大度数称为树的度。
例如:结点 B 的度为 2 ; 结点 D 的度为 3 , 树的度为 3 。
度大于 0 的结点称为 分支结点(又称为非终端结点) ;
度为 0 的(没有子女结点)的结点称为叶子结点(又称为终端结点)
在分支结点中,每个结点的分支树就是该结点的度。 ### 结点的深度、高度和层次
结点的层次从树根开始定义,根结点为第 1 层(有些教材中将根结点定义为第 0 层),它的子结点为第
2 层,依次类推。
结点的深度是从根结点开始自顶向下逐层累加的。
结点的高度是从叶结点开始自底向上逐层累加的。
树的高度(又称为深度)是树中结点的最大层数。上图中树的高度为 4 。
有序树和无序树:
树中结点的子树从左到右是有次序的,不能交换,这样的树叫做有序树。在有序树中,一个结点其子结点
按从左到右顺序出现是有关联的。反之则称为无序树。
在上图中,若将子结点位置互换,则变成一颗不同的树。
路径和路径长度:
树中两个结点之间的路径是由这两个结点之间所经过的结点序列构成的;
路径长度是路径上所经过的边的个数。
注意:由于树中分支是有向的,即从双亲结点指向孩子结点,所以树中的路径是从上向下的,同一个双亲
结点的两个孩子结点之间不存在路径。
森林:
森林是 m ( m >= 0) 棵互不相交的树的集合。森林的概念与树的概念十分相近,因为只要把树的根结点
删除就成了森林。反之,只要给 n 棵独立的树加上一个结点,并把这 n 棵树作为该结点的子树,则森林就变
成了树。
树的前序遍历后序遍历中序遍历算法
package com.company.tree;
/**
* @author : CLEAR Li
* @version : V1.0
* @className : TreeNode
* @packageName : com.company.tree
* @description : 一般类
* @date : 2020-05-10 11:22
**/
public class TreeNode {
int value;
TreeNode leftNode;
TreeNode rightNode;
//前序遍历
public void frontShow(){
System.out.print(value+" ");
if (leftNode!=null){
leftNode.frontShow();
}
if (rightNode!=null){
rightNode.frontShow();
}
}
//中序遍历
public void midShow(){
if (leftNode!=null){
leftNode.midShow();
}
System.out.print(value+" ");
if (rightNode!=null){
rightNode.midShow();
}
}
//后序遍历
public void afterShow(){
if (leftNode!=null){
leftNode.afterShow();
}
if (rightNode!=null){
rightNode.afterShow();
}
System.out.print(value+" ");
}
public TreeNode(int value) {
this.value = value;
}
public TreeNode() {
}
public void setValue(int value) {
this.value = value;
}
public int getValue() {
return value;
}
public TreeNode getLeftNode() {
return leftNode;
}
public void setLeftNode(TreeNode leftNode) {
this.leftNode = leftNode;
}
public TreeNode getRightNode() {
return rightNode;
}
public void setRightNode(TreeNode rightNode) {
this.rightNode = rightNode;
}
}
测试类
package com.company.tree;
/**
* @author : CLEAR Li
* @version : V1.0
* @className : BinarryTree
* @packageName : com.company.tree
* @description : 一般类
* @date : 2020-05-10 11:18
**/
public class BinaryTree {
TreeNode root;
public void setRoot(TreeNode root) {
this.root = root;
}
public TreeNode getRoot() {
return root;
}
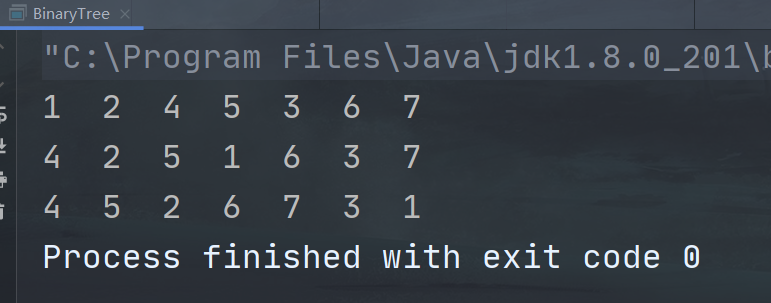
public static void main(String[] args) {
BinaryTree binaryTree = new BinaryTree();
//创建一个根节点
TreeNode root = new TreeNode(1);
//
binaryTree.setRoot(root);
//创建两个节点
TreeNode rootL = new TreeNode(2);
root.setLeftNode(rootL);
TreeNode rootR = new TreeNode(3);
root.setRightNode(rootR);
//为第二层的左节点创建两个子节点
rootL.setLeftNode(new TreeNode(4));
rootL.setRightNode(new TreeNode(5));
rootR.setLeftNode(new TreeNode(6));
rootR.setRightNode(new TreeNode(7));
//遍历这个树
//binaryTree.
binaryTree.root.frontShow();
System.out.println();
binaryTree.root.midShow();
System.out.println();
binaryTree.root.afterShow();
}
}
结果显示